Receiver Operator Characteristic (ROC) 或稱 ROC 曲線, 它是一個二維圖形

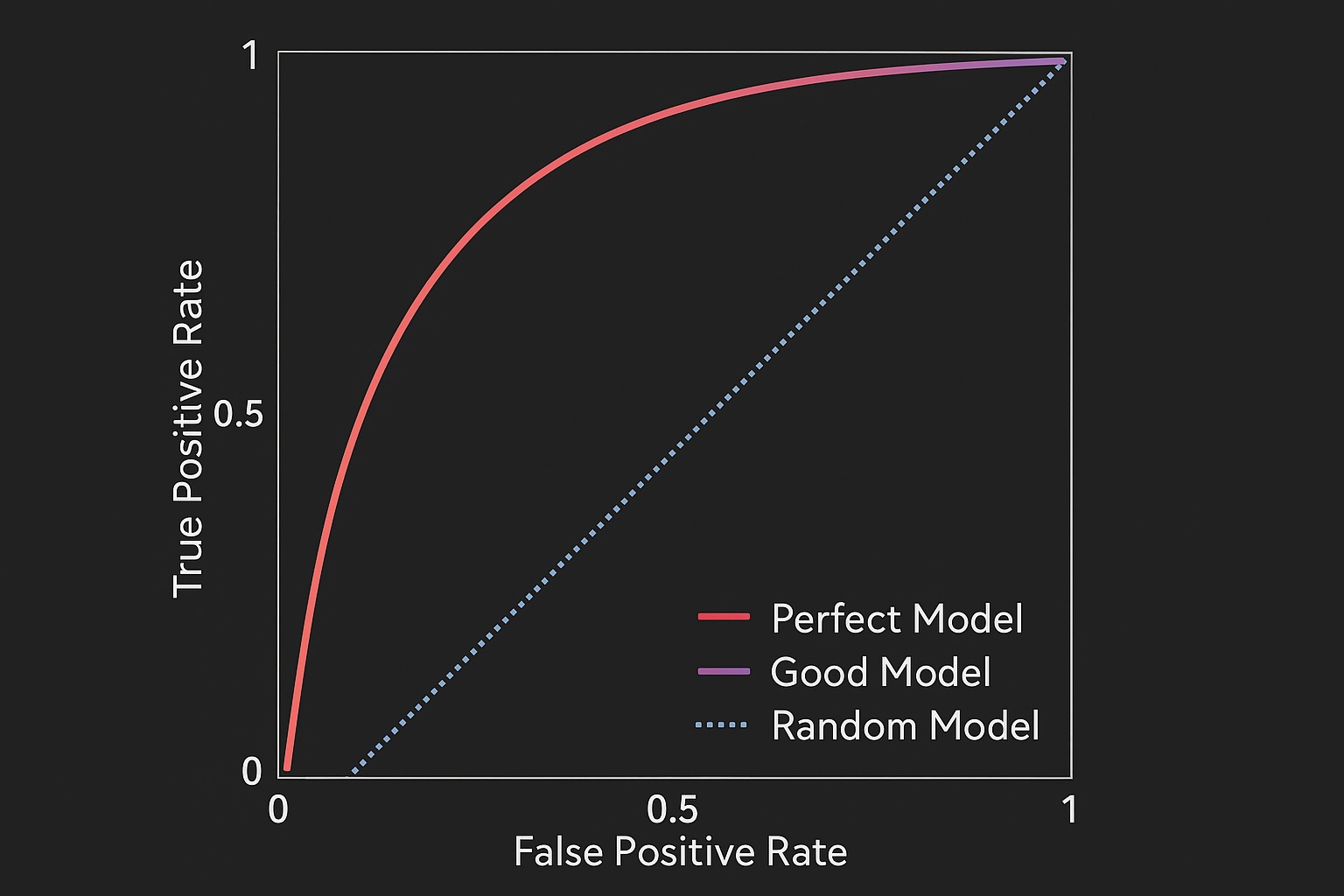
它的 X 軸和 Y 軸分別代表
Y 軸：真正率 (True Positive Rate, TPR), 也稱為： 敏感度 (Sensitivity) 或 召回率 (Recall)
– 在所有「真正是正類」的樣本中，模型成功抓出來（預測為正）的比例
– 我們希望這個值越高越好（越接近 1 越好）
– 公式: $TPR = \frac{TP}{TP + FN}$

X 軸：偽正率 (False Positive Rate, FPR)
– 在所有「真正是負類」的樣本中，模型錯誤抓出來（預測為正）的比例,（即「誤報率」）
– 我們希望這個值越低越好（越接近 0 越好）
– 公式: $FPR = \frac{FP}{FP + TN}$

必須知道大部分的分類模型（如邏輯迴歸）並不是直接輸出「類別 A」或「類別 B」,它們會輸出一個機率值（例如 0 到 1 之間）,我們需要設定一個「門檻」(threshold) 來決定如何分類, 例如，設定門檻為 0.5。如果模型輸出 0.7，我們就判為「正類 (Positive)」；如果輸出 0.3，就判為「負類 (Negative)」

那麼 0.5 真的是最好的門檻嗎？如果這是一個抓捕恐怖份子的模型，我們寧願抓錯 (FPR 高), 也不願放過（TPR 低）, 這時我們可能會把門檻降到 0.1. 如果這是一個發送優惠券的模型，我們不希望發給不想買的人（FPR 高），這時我們可能會把門檻提高到 0.8, 而 ROC 曲線就是在描繪：當我們「滑動」這個門檻（從 0.0 到 1.0）時，模型的表現會如何變化.

這個二維曲線中有幾個重要的關鍵點 =>
(0, 0) 點: 左下角, 代表門檻設在 1.0, 模型將所有樣本都預測為「負類」
TPR = 0 (一個正類都沒抓到), FPR = 0 (一個負類都沒抓錯)

(1, 1) 點: 右上角, 代表門檻設在 0.0, 模型將所有樣本都預測為「正類」
TPR = 1 (所有正類都抓到了), FPR = 1 (所有負類都抓錯了)

對角線 (y=x): 從 (0,0) 到 (1,1) 的虛線, 這代表一個「隨機猜測」的模型（例如丟硬幣）. 它的 TPR 永遠等於 FPR, 任何模型的 ROC 曲線都應該在這條線的上方。如果在下方，表示模型比亂猜還差。

一個好的模型，其 ROC 曲線會盡可能地「貼近」左上角 (0, 1).
左上角 (0, 1) 代表一個完美的模型：FPR = 0 (沒有誤報)，且 TPR = 1 (全部抓到)

光看一條曲線很難直接比較兩個模型的好壞，因此我們計算曲線下的面積，稱為 AUC (Area Under the Curve)

AUC 是一個單一的數值（介於 0 和 1 之間）, 用來總結 ROC 曲線的整體表現
AUC = 1.0: 完美的分類器
AUC = 0.5: 等同於隨機猜測
AUC < 0.5: 比隨機猜測還差
AUC > 0.8: 通常被認為是一個良好 (Good) 的模型
AUC > 0.9: 通常被認為是一個優秀 (Excellent) 的模型

AUC 在統計學有個解釋: AUC 的值, 等於「模型從(postive)正類樣本中隨機抽一個，其機率分數 > 從負類樣本中隨機抽一個的機率分數」的機率, 簡單來說，AUC 衡量的是模型將「正類」排在「負類」前面的能力. 它衡量的是模型的「排序能力」, 而不是單純的「分類準確度」

總結

ROC 曲線: 視覺化呈現模型在所有門檻下的「抓對能力 (TPR)」與「誤報風險 (FPR)」之間的權衡

AUC 值： 一個單一數值，總結模型「區分正負類別」的整體能力, 它不受特定門檻選擇的影響，因此是評估模型好壞時非常穩健且常用的